목차
[선택 정렬]
리스트에서 최소 값을 찾은 후 리스트의 맨 앞에 있는 값과 교환하는 방식
부분 리스트에 대해 모든 원소를 순회할 때 까지 반복한다.
- 시간복잡도:
정렬 방법

초기상태. 아래값으로 초기 세팅이 진행된다.
i = 0
idx = i
j = i+1

arr[idx]와 arr[j]값을 비교하여 j의 값이 더 작은 경우 idx 값을 j로 변경한다.

j를 전진시키면서 arr[idx]와 arr[j] 값을 비교한다. 이번에는 arr[j] 값이 더 크므로 idx를 유지한다.

다음 비교를 진행하는데 마찬가지로 arr[j]값이 더 크므로 idx는 유지한다.


배열의 끝까지 비교를 진행한다.

j가 끝까지 도착했을 때 idx와 i값을 교환해준다. 이렇게하면 순회 한 번이 끝난다.

다음 순회를 위해 i, idx, j값을 초기화 한다.

마찬가지로 arr[idx]와 arr[j]를 비교한다. arr[j]가 더 작으므로 idx 값을 변경한다.


j를 이동하여 arr[idx]와 arr[j] 값을 비교한다. arr[j]가 더 작으므로 idx값을 변경해준다.

j를 이동하여 arr[idx]와 arr[j] 값을 비교한다. arr[j] 더 크므로 idx는 유지한다.

j를 전진하여 arr[idx]와 arr[j]를 비교한다. 마찬가지로 7<15이므로 idx값은 유지한다.

순회를 마쳤으므로 arr[idx]와 arr[i]를 교환한다.

다음 순회를 시작한다.
arr[idx]와 arr[j] 값을 비교한다. arr[j]가 더 크므로 인덱스는 유지한다.

j를 이동하여 비교한다. 마찬가지로 arr[idx]와 arr[j] 값을 비교한다. arr[j]가 더 크므로 인덱스는 유지한다.

j를 이동하여 비교한다. 마찬가지로 arr[idx]와 arr[j] 값을 비교한다. arr[j]가 더 크므로 인덱스는 유지한다.

순회가 끝났으니 arr[idx]와 arr[i]를 교환한다. 자리가 같으므로 결과는 동일하다.
...반복...

모든 순회가 완료되면 정렬이 완료된다.
코드
public class SelectionSort {
static int[] solution(int n, int[] arr) {
for (int i = 0; i < n-1; i++) {
int idx = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[idx]) {
idx = j;
}
}
int temp = arr[i];
arr[i] = arr[idx];
arr[idx] = temp;
}
return arr;
}
public static void main(String[] args) {
int n = 6;
int[] arr = {13, 5, 11, 7, 23, 15};
int[] answer = solution(n, arr);
for (int a : answer) {
System.out.print(a+" ");
}
}
}
[버블 정렬]
인접한 두 원소를 비교하여 작은 값이 앞으로 오도록 정렬하는 방법.
- 시간 복잡도: O(n^2)
정렬 방법
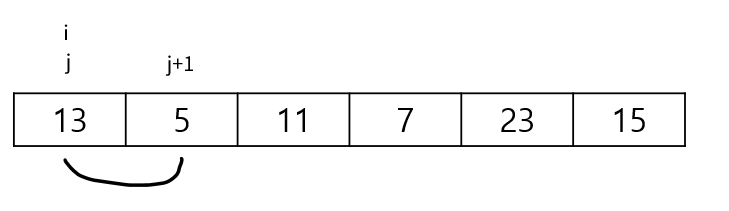

인접한 두 값인 13과 5를 비교한다. 5가 더 작으니 위치를 교환해준다.


다음으로 인접한 13과 11을 비교한다. 11이 더 작으니 위치를 교환한다.
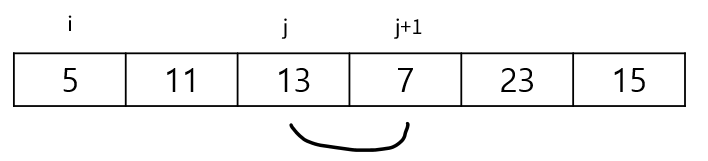

다음으로 인접한 13과 7을 비교한다. 7이 더 작으니 위치를 교환한다.

다음으로 인접한 13과 23을 비교한다. 이번에는 23이 더 크므로 교환하지 않는다.


다음으로 인접한 23과 15를 비교한다. 15가 더 작으니 위치를 교환한다.


순회가 끝났으니 다시 순회를 시작한다. 11과 7을 비교한다. 7이 더 작으므로 위치를 교환한다.

다음으로 인접한 11과 13을 비교한다. 13이 더 크므로 교환하지 않는다.

다음으로 인접한 13과 15를 비교한다. 15가 더 크니 교환하지 않는다.

다음으로 15와 23을 비교한다. 23이 더 크므로 교환하지 않는다.
...반복

코드
public class BubbleSort {
static int[] solution(int n, int[] arr) {
for (int i = 0; i < n -1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
return arr;
}
public static void main(String[] args) {
int n = 6;
int[] arr = {13, 5, 11, 7, 23, 15};
int[] answer = solution(n, arr);
for (int a : answer) {
System.out.print(a+" ");
}
}
}
[삽입 정렬]
새로운 원소를 이전까지 정렬된 원소 사이에 삽입시키는 방법
- 시간복잡도: 최선의 경우 O(n), 최악의 경우 O(n^2)
정렬 방법

i는 1부터 시작하고, j는 i-1부터 시작하며 tmp 값은 i값으로 초기화해놓는다.

이 상태에서 arr[j]가 tmp보다 크면 arr[j]값을 뒤로 밀게 된다. arr[j]의 11이 tmp인 7보다 크므로 arr[j]값을 뒤로 밀어야한다.
그럼 위처럼 된다.

그 다음 j는 -1이 되어서 순회가 끝난다. 그럼 j+1 자리에 tmp를 넣어준다.

다음순회를 시작한다. i를 전진하고, j를 i-1로 설정한다. tmp는 i의 값인 5가 된다.

arr[j]의 11과 tmp 5값을 비교한다. 11이 더 크므로 11을 또 뒤로 밀어야 한다.


j를 한 칸 앞으로 당겨 7과 5를 비교한다. 7이 더 크므로 7을 뒤로 민다.
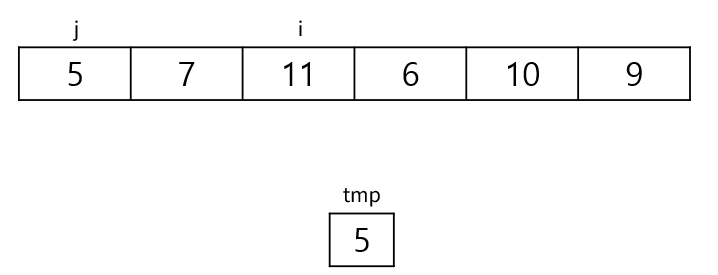
j의 순회가 끝났으므로 j의 자리에 tmp값을 넣는다.

다음 순회를 시작한다. tmp값은 6이 된다.

11과 6을 비교한다. 11이 더 크므로 11을 뒤로 민다.

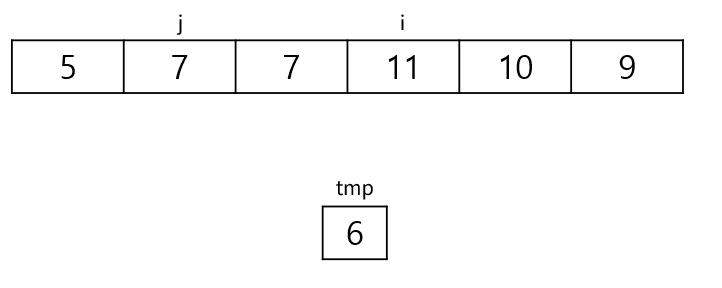
다음으로 7과 6을 비교한다. 7이 크므로 7을 뒤로 민다.

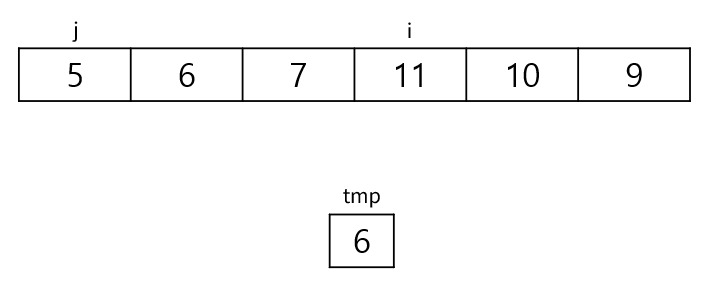
다음으로 5와 6을 비교한다. 이번에는 5가 더 작으므로 뒤로 밀 필요가 없다. 여기서 바로 break하고 j+1위치에 tmp값을 삽입한다.
...반복...

코드
public class InsertionSort {
static int[] solution(int n, int[] arr) {
for (int i = 1; i < n; i++) {
int tmp = arr[i];
int j = i-1;
for (;j > 0; j--) {
if (arr[j] > tmp) {
arr[j + 1] = arr[j];
} else {
break;
}
}
arr[j+1] = tmp;
}
return arr;
}
public static void main(String[] args) {
int n = 6;
int[] arr = {5, 6, 7, 9, 10, 11};
int[] answer = solution(n, arr);
for (int a : answer) {
System.out.print(a+" ");
}
}
}
[병합 정렬 (Merge Sort)]
분할 정복 (Devide and Conquer) 기법과 재귀 알고리즘을 활용한 정렬 알고리즘.
주어진 배열을 원소가 하나 남을 때까지 둘로 쪼갠 후에 다시 크기 순으로 재배열 하면서 원래 크기의 배열로 합치는 방식
- 시간 복잡도: O(n log n)
정렬 방법

코드
public class MergeSort {
static int[] mergeSort(int[] arr) {
if (arr.length < 2) return arr;
int mid = arr.length / 2;
int[] left = mergeSort(Arrays.copyOfRange(arr, 0, mid));
int[] right = mergeSort(Arrays.copyOfRange(arr, mid, arr.length));
int[] mergedArr = new int[arr.length];
int m = 0, l = 0, h = 0;
while (l < left.length && h < right.length) {
if (left[l] < right[h])
mergedArr[m++] = left[l++];
else
mergedArr[m++] = right[h++];
}
// 남은 원소 추가
while (l < left.length) {
mergedArr[m++] = left[l++];
}
while (h < right.length) {
mergedArr[m++] = right[h++];
}
return mergedArr;
}
public static void main(String[] args) {
int[] arr = {6, 5, 3, 1, 8, 7, 2, 4};
int[] answer = mergeSort(arr);
for (int a : answer) {
System.out.print(a+" ");
}
}
}
[퀵 정렬]
분할 정복 알고리즘 중 하나.
주어진 배열에서 하나의 element를 선정하고 이를 pivot으로 삼는다.
배열 내부의 모든 값들을 검사하면서 pivot 값보다 작으면 왼쪽에 크면 오른쪽에 배치한다.
이렇게하면 배열이 두 부분으로 나뉜다. 나뉜 2개의 배열에서 새로운 피벗을 만들고 또 2개의 배열로 쪼갠다.
배열을 쪼갤 수 없을 때 까지 진행한다.
- 시간 복잡도: O(nlogn), 최악 O(n^2)
정렬 방법

pivot을 선정하고 배열을 탐색하기 위해 low와 high를 피벗을 제외한 배열 끝에 배치한다.

low를 이동하면서 배열을 검사하는데 pivot의 값이 low의 값보다 작아야 계속 진행한다.
low의 9과 5를 비교한다. 피벗의 값 5보다 low의 값이 더 크므로 멈춘다.

다음으로 high를 이동한다. high는 pivot의 값보다 커야 계속진행한다.
1과 5를 비교했을 때 high는 pivot의 값보다 크지 않아서 더 진행할 수 없다.

이 시점에서 low와 high를 봤을 때 위치가 역전되지 않았으면 두 요소만 교환한다.

다시 low를 이동한다. low는 pivot보다 작아야 이동한다고 했다. 하지만 pivot보다 크므로 low는 중단된다.

high를 다시 진행한다. high는 pivot보다 커야 진행될 수 있다. 하지만 3이므로 5보다 작아서 high도 멈춘다.

low와 high를 비교했을 때 위치가 역전되지 않았다. 그러므로 둘의 값을 교환한다.

low를 계속 진행한다. pivot보다 작아야 계속 진행할 수 있다. 하지만 피벗보다 커서 또 중단된다.

high도 이동하는데 pivot보다 크지 않아서 중단된다.
그런데 이번에는 low와 high의 위치가 변경되었다. 이 경우에는 값을 교환하지 않는다.

이 경우에는 피벗과 high의 값을 교환한다.

다음으로 pivot을 중심으로 배열을 쪼갠다.

다음으로 똑같이 피벗을 선정하고 정렬을 수행한다.

왼쪽 배열을 정렬해보자. low부터 수행한다. low는 pivot보다 작아야 진행할 수 있다고 했다.
끝까지 진행할 수 있어서 low는 멈춘다.

다음으로 high를 진행한다. high는 pivot보다 커야 진행할 수 있다. 하지만 1이 3보다 작으므로 바로 멈춘다.
이 때 high와 low의 위치가 역전되었다.
위치가 역전된 경우 high와 pivot을 교환해준다.

pivot을 중심으로 쪼갠다.

우측 배열부터보면 더 이상 정렬할 부분이 없으니 중단할 수 있다.

왼쪽 배열을 보면 low는 pivot보다 작아야 진행할 수 있는데 더 크니까 중단한다. high는 pivot보다 커서 진행했으나 low와 high의 위치가 바뀌었고, high와 pivot의 위치를 교환한다. 결론적으로 위와같은 그림이 된다.
pivot을 기준으로 쪼개면 [1,2]만 남고 더 이상 정렬할게 없으니 나머지 부분에 대해서도 반복하면 된다.
...반복...
코드
public class QuickSort {
static int partition (int[] arr, int p, int r){
int low, high;
int pivot = arr[p]; // pivot 값 설정
low = p + 1;
high = r;
while(low <= high){
while(arr[low] < pivot) low++;
while(arr[high] > pivot) high--;
if (low <= high){
int temp = arr[low];
arr[low] = arr[high];
arr[high] = temp;
}
}
int temp = arr[p];
arr[p] = arr[high];
arr[high] = temp;
return high;
}
static void quickSort(int[] arr, int left, int right){
if (left < right){
int pivot = partition(arr, left, right);
quickSort(arr, left, pivot-1);
quickSort(arr, pivot+1, right);
}
}
public static void main(String[] args) {
int[] arr = {3, 2, 1, 5, 7, 9, 6};
quickSort(arr, 0, arr.length - 1);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}
[참조]
https://jeonyeohun.tistory.com/102
[알고리즘 정리] 퀵정렬(Quick Sort)
퀵소트 퀵 정렬은 이름 그대로 매우 빠르게 정렬을 수행하는 알고리즘이다. 기본적으로 분할정복의 성격을 가지고 있고 실제로도 많이 사용되는 대표적인 정렬 알고리즘이다. 동시에 자료구조
jeonyeohun.tistory.com